堆(优先级队列)
目录
🥬堆的性质
堆逻辑上是一棵完全二叉树,堆物理上是保存在数组中 。
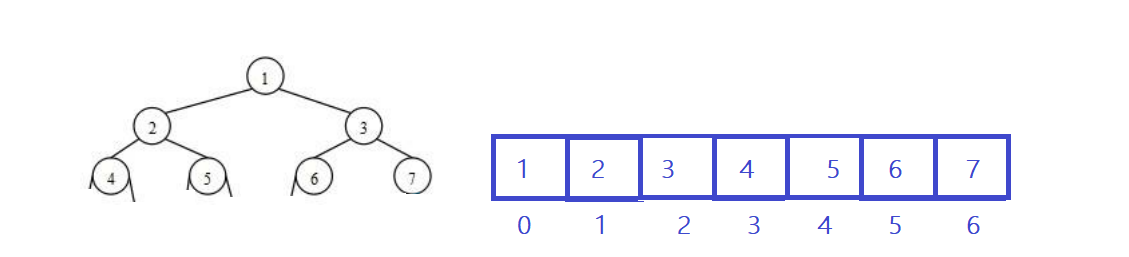
总结:一颗完全二叉树以层序遍历方式放入数组中存储,这种方式的主要用法就是堆的表示。
并且 如果已知父亲(parent) 的下标,则:
左孩子(left) 下标 = 2 * parent + 1;
右孩子(right) 下标 = 2 * parent + 2;
已知孩子(不区分左右)(child)下标,则:
双亲(parent) 下标 = (child - 1) / 2;
🥬堆的分类
大堆:根节点大于左右两个子节点的完全二叉树 (父亲节点大于其子节点),叫做大堆,或者大根堆,或者最大堆 。
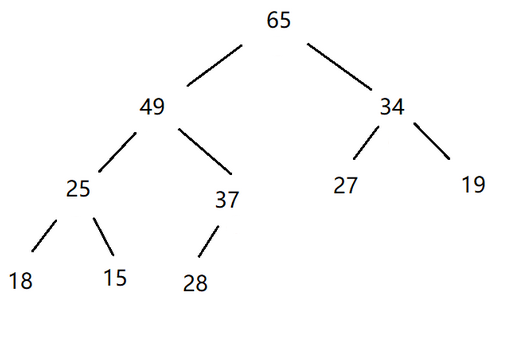
小堆:根节点小于左右两个子节点的完全二叉树叫
小堆(父亲节点小于其子节点),或者小根堆,或者最小堆。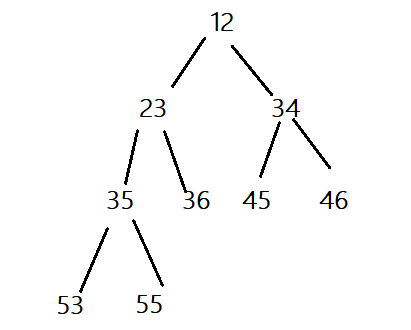
🥬堆的向下调整
现在有一个数组,逻辑上是完全二叉树,我们通过从根节点开始的向下调整算法可以把它调整成一个小堆或者大堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
以小堆为例:
1、先让左右孩子结点比较,取最小值。
2、用较小的那个孩子结点与父亲节点比较,如果孩子结点<父亲节点,交换,反之,不交换。
3、循环往复,如果孩子结点的下标越界,则说明已经到了最后,就结束。 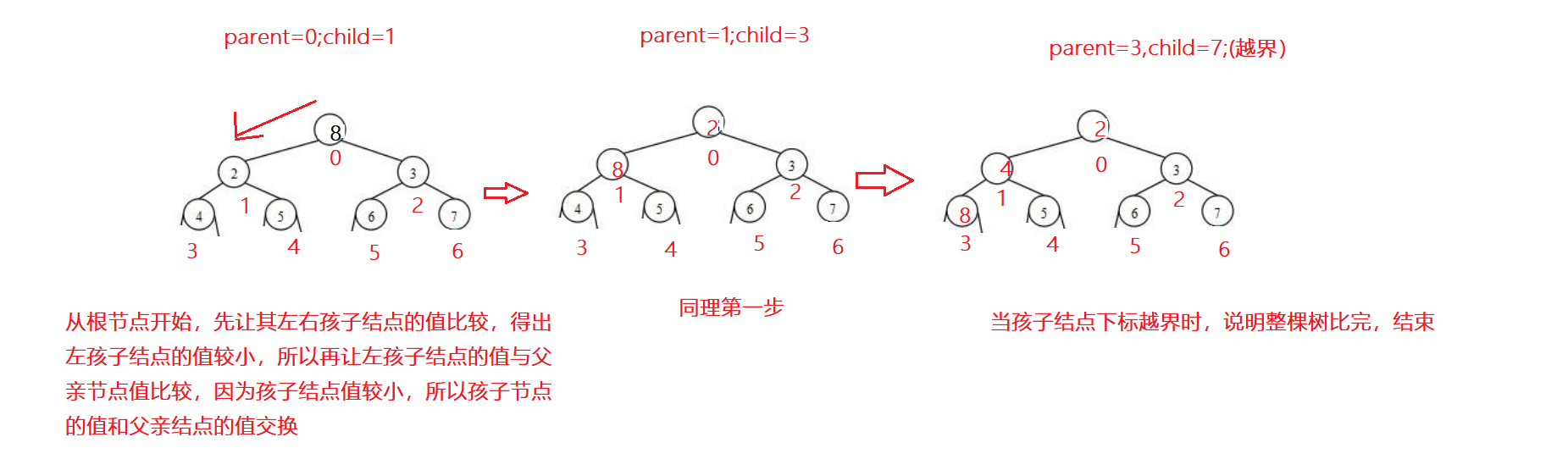
//parent: 每棵树的根节点
//len: 每棵树的调整的结束位置
public void shiftDown(int parent,int len){
int child=parent*2+1; //因为堆是完全二叉树,没有左孩子就一定没有右孩子,所以最起码是有左孩子的,至少有1个孩子
while(child<len){
if(child+1<len && elem[child]<elem[child+1]){
child++;//两孩子结点比较取较小值
}
if(elem[child]<elem[parent]){
int tmp=elem[parent];
elem[parent]=elem[child];
elem[child]=tmp;
parent=child;
child=parent*2+1;
}else{
break;
}
}
}🥬堆的建立
给出一个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆(左右子树不满足都是大堆或者小堆),现在我们通过算法,把它构建成一个堆(大堆或者小堆)。该怎么做呢?这里我们从倒数的第一个非叶子节点的子树开始调整,一直调整到根节点的树,就可以调整成堆。 这里我们就要用到刚才写的向下调整。
public void creatHeap(int[] arr){
for(int i=0;i<arr.length;i++){
elem[i]=arr[i];
useSize++;
}
for(int parent=(useSize-1-1)/2;parent>=0;parent--){//数组下标从0开始
shiftDown(parent,useSize);
}
}
建堆的空间复杂度为O(N),因为堆为一棵完全二叉树,满二叉树也是一种完全二叉树,我们用满二叉树(最坏情况下)来证明。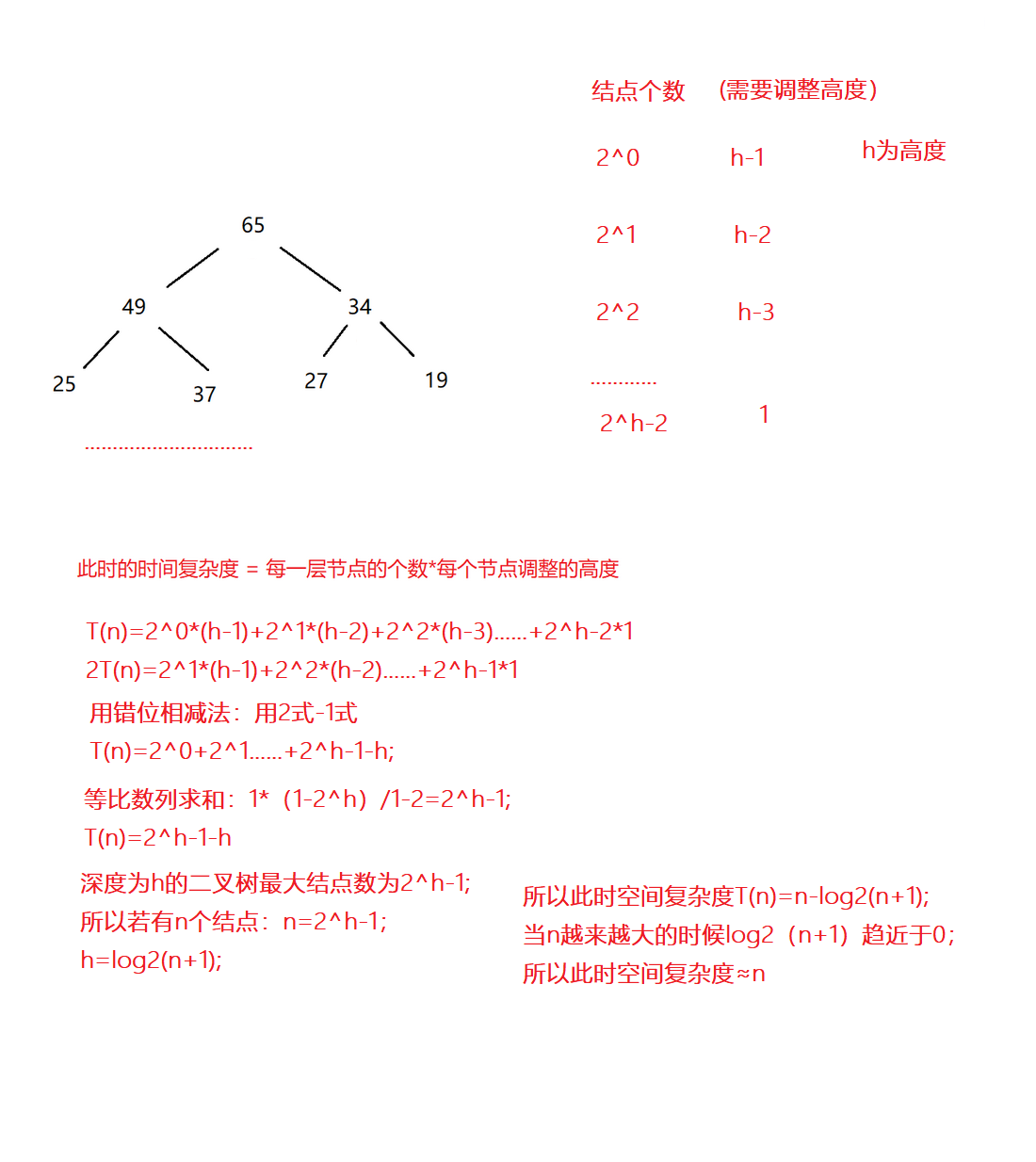
🥬堆得向上调整
现在有一个堆,我们需要在堆的末尾插入数据,再对其进行调整,使其仍然保持堆的结构,这就是向上调整。
以大堆为例:
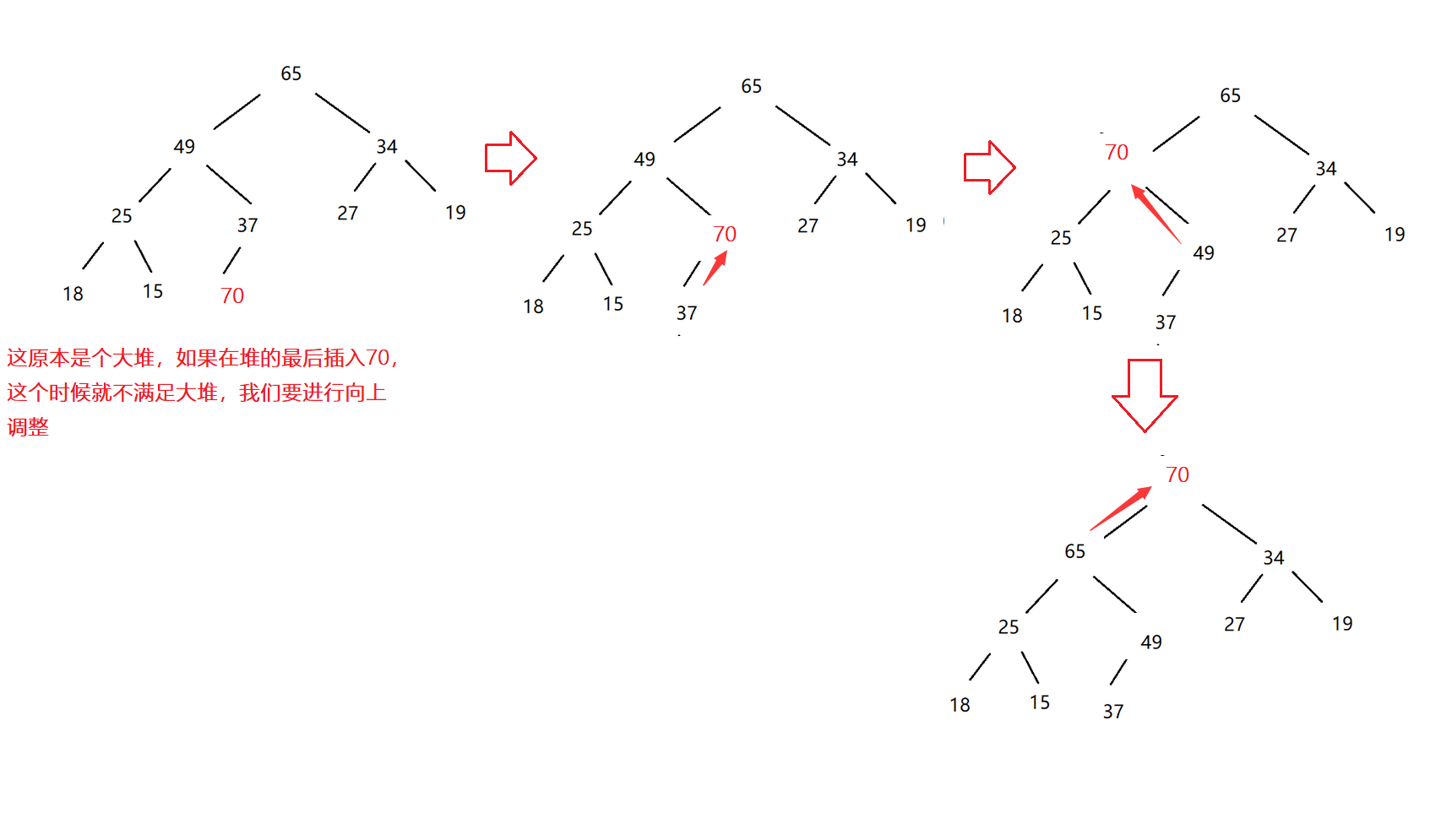
代码示例:
public void shiftup(int child){
int parent=(child-1)/2;
while(child>0){
if(elem[child]>elem[parent]){
int tmp=elem[parent];
elem[parent]=elem[child];
elem[child]=tmp;
child=parent;
parent=(child-1)/2;
}else{
break;
}
}
}🥬堆的常用操作
🍌入队列
往堆里面加入元素,就是往最后一个位置加入,然后在进行向上调整
public boolean isFull(){
return elem.length==useSize;
}
public void offer(int val){
if(isFull()){
elem= Arrays.copyOf(elem,2*elem.length);//扩容
}
elem[useSize++]=val;
shiftup(useSize-1);
}🍌获取队首元素
public int peek() {
if (isEmpty()) {
throw new RuntimeException("优先级队列为空");
}
return elem[0];
}🥬TopK 问题
给你6个数据,求前3个最大数据。这时候我们用堆怎么做的?
解题思路:
1、如果求前K个最大的元素,要建一个小根堆。
2、如果求前K个最小的元素,要建一个大根堆。
3、第K大的元素。建一个小堆,堆顶元素就是第K大的元素。
4、第K小的元素。建一个大堆,堆顶元素就是第K大的元素。
🍌举个例子:求前n个最大数据
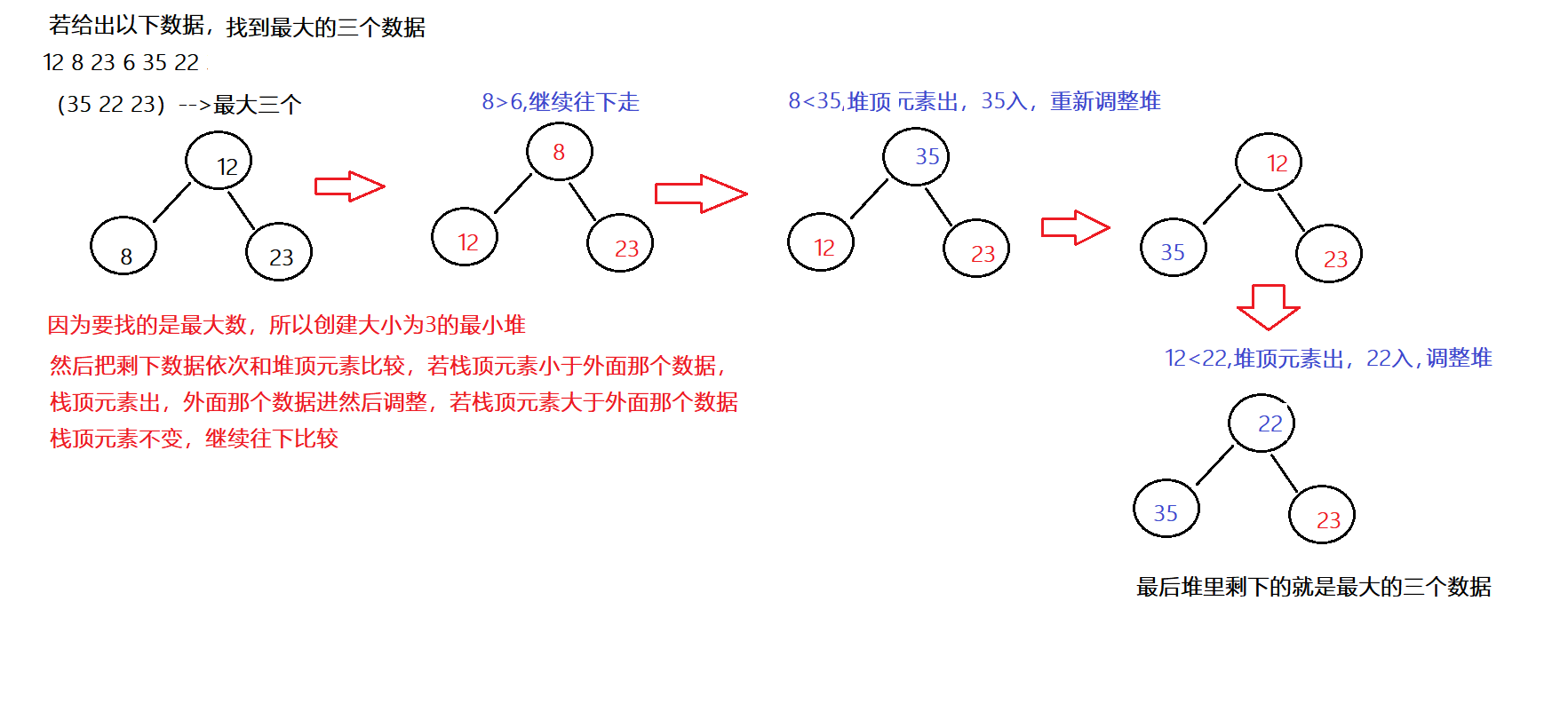
代码示例:
public static int[] topK(int[] array,int k){
//创建一个大小为K的小根堆
PriorityQueue<Integer> minHeap=new PriorityQueue<>(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1-o2;
}
});
//遍历数组中元素,将前k个元素放入队列中
for(int i=0;i<array.length;i++){
if(minHeap.size()<k){
minHeap.offer(array[i]);
}else{
//从k+1个元素开始,分别和堆顶元素比较
int top=minHeap.peek();
if(array[i]>top){
//先弹出后存入
minHeap.poll();
minHeap.offer(array[i]);
}
}
}
//将堆中元素放入数组中
int[] tmp=new int[k];
for(int i=0;i< tmp.length;i++){
int top=minHeap.poll();
tmp[i]=top;
}
return tmp;
}
public static void main(String[] args) {
int[] array={12,8,23,6,35,22};
int[] tmp=topK(array,3);
System.out.println(Arrays.toString(tmp));
}
结果:
🍌数组排序
再者说如果要对一个数组进行从小到大排序,要借助大根堆还是小根堆呢?
---->大根堆
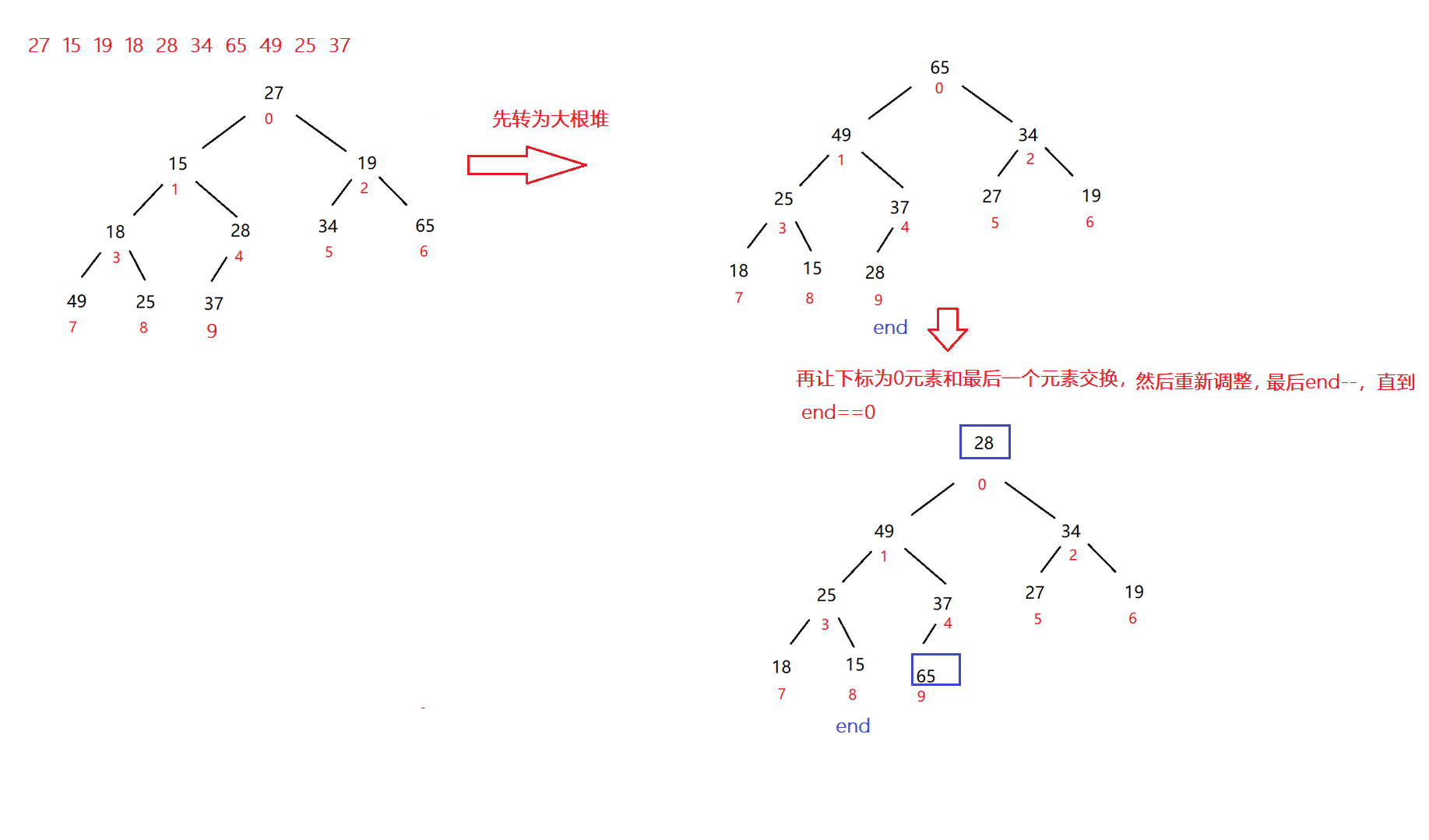
public void heapSort(){
int end=useSize-1;
while(end>0){
int tmp=elem[0];
elem[0]=elem[end];
elem[end]=tmp;
shiftDown(0,end);//假设这里向下调整为大根堆
end--;
}
}🥬小结
以上就是今天的内容了,有什么问题可以在评论区留言✌✌✌
