情景回顾

平时在聊天谈论算法时候，发现很多人并不清楚算法的时间复杂度怎么计算，一些稍微复杂的算法时间复杂度问题，就无法算出时间复杂度。那么我在今天的文章里去解答这些问题

时间复杂度与空间复杂度

时间复杂度

执行这个算法所需要的计算工作量

1. 
   

2. 随着输入数据的规模，时间也不断增长，那么时间复杂度就是一个算法性能可观的数据。

   
   

3. 由于实际算法的时间会根据机器的性能，软件的环境导致不同的结果，那么通常都是预估这个时间。

   
   

4. 算法花费时间与执行语句次数成正比，执行次数称为语句频度或时间频度。记为T(n)

   
   

5. 在时间频度中，n称为问题的规模，当n不断变化时，它所呈现出来的规律，称之为时间复杂度

   
   

说明：

• 
  
• 若算法中的语句执行次数为一个常数，则时间复杂度为o(1)
• 不同算法的时间频度不一样，但他们的时间复杂度却可能是一样的。

例如：T(n)=2n+4+n^2
T(n)=n+8 + 4n^2
很明显时间频度不同，但是他们时间复杂度是相同的 都为O(n^2)

计算时间复杂度步骤：

1. 
   
2. 找出算法中的基本语句（执行次数最多的那条语句就是基本语句，通常是最内层循环的循环体。）
3. 计算基本语句的执行次数的数量级（只要保证基本语句执行次数的函数中的最高次幂正确即可，可以忽略所有低次幂和最高次幂的系数。这样能够简化算法分析，并且使注意力集中在最重要的一点上：增长率。）
4. 用大Ο记号表示算法的时间性能。

原则：

1. 
   
2. 如果运行时间是常数量级，用常数1表示
3. 只保留时间函数中的最高阶项
4. 如果最高阶项存在，则省去最高阶项前面的系数

例1：

        for(i in 0..n){

            a++

        }

        for(i in 0..n){

            for(i in 0..n){

                a++

            }

        }

在看这个算法时候，很明显时间 复杂度为O(n+n^2) 但要留下最高阶 也就是O(n^2)
例2：

        for(i in 0..n){

            a++

            b++

            c++

        }

在看这个算法时候，很明显时间 复杂度为O(3n) 但要抹掉常数3 也就是O(n)

例3：

        var i = 1

        while (i < n) {

           a++

           b++

           c++

           i *= 2

        }

在看这个算法时候，很明显时间 复杂度为O(3logn) 但要抹掉常数3 也就是O(logn)

例4：

           a++

           b++

           c++

在看这个算法时候，很明显时间 复杂度为O(3) 常数级别的算法都为O(1)

平衡二叉搜索树的时间复杂度是怎么计算出来的呢（重点）

为啥我要加个重点标识呢？因为很多人都不晓得平衡二叉搜索树的O(logn)是咋计算出来的，今天我给大家掰扯掰扯

假设生成高度树h的节点数是n(h) ，高度为h-1的节点数为n(h-1)
他们之间的关系为 n(h) = n(h-1)+n(h-1)+1
n(h) = 2n(h-1)+1
n(h) 约等于 2n(h-1)
注意的一点 n(h-1) 几乎是一半的节点数目
基准点 h(0) = 1 h(1) = 3
依次类推
n(h) 约等于 h^2
那么
n(h) = h^2
那么
h = log2n
则平衡二叉搜索树的时间复杂度 O(logn)

时间复杂度比较

常见的时问复杂度如表所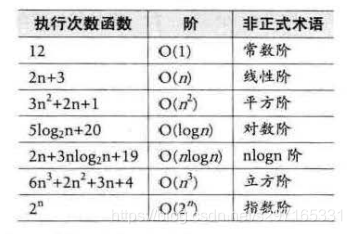

常用的时间复杂度所耗费的时间从小到大依次是：

复杂度在1s内，能处理的数据量大小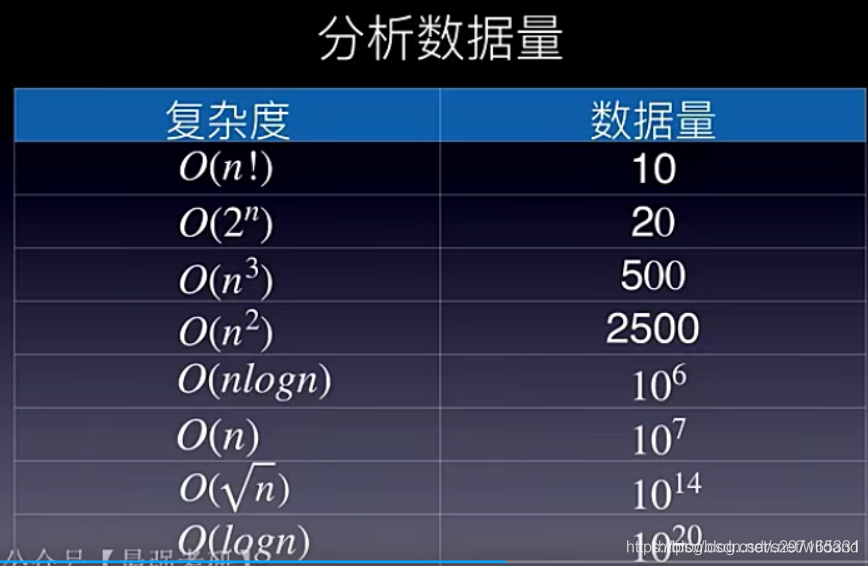

复杂度分析的4个概念

为什么要引入这4个概念？

如何分析平均、均摊时间复杂度？

最坏情况与平均情况

我们查找一个有n 个随机数字数组中的某个数字，最好的情况是第一个数字就是，那么算法的时间复杂度为O(1)，但也有可能这个数字就在最后一个位置上待着，那么算法的时间复杂度就是O(n)，这是最坏的一种情况了。

最坏情况运行时间是一种保证，那就是运行时间将不会再坏了。 在应用中，这是一种最重要的需求， 通常， 除非特别指定， 我们提到的运行时间都是最坏情况的运行时间。

而平均运行时间也就是从概率的角度看， 这个数字在每一个位置的可能性是相同的，所以平均的查找时间为n/2次后发现这个目标元素。平均运行时间是所有情况中最有意义的，因为它是期望的运行时间。也就是说，我们运行一段程序代码时，是希望看到平均运行时间的。可现实中，平均运行时间很难通过分析得到，一般都是通过运行一定数量的实验数据后估算出来的。一般在没有特殊说明的情况下，都是指最坏时间复杂度。

空间复杂度

执行这个算法所需要的内存空间

例

        var m = arrayOfNulls<Int>(n)

        for(i in 0..n){

            a++

            m[i] = a

        }

空间复杂度为 O(n)

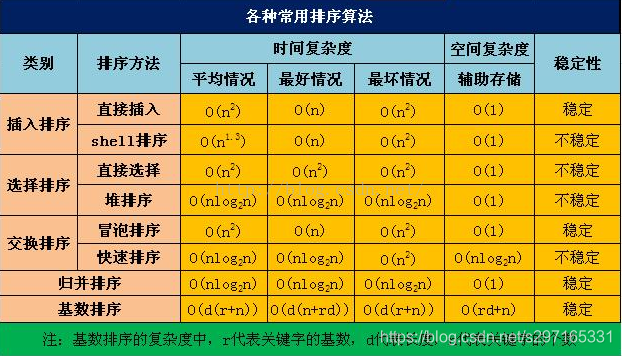
常用算法的时间复杂度和空间复杂度