一文理解贝塞尔曲线

贝塞尔曲线的来源

贝塞尔曲线最早是由贝塞尔在1962年提出来的，目的是获取汽车的外形。贝塞尔曲线看上去非常复杂，其实想法非常简单，（如下图1所示）就是先用折线先绘制出大致的轮廓，然后用曲线来逼近。

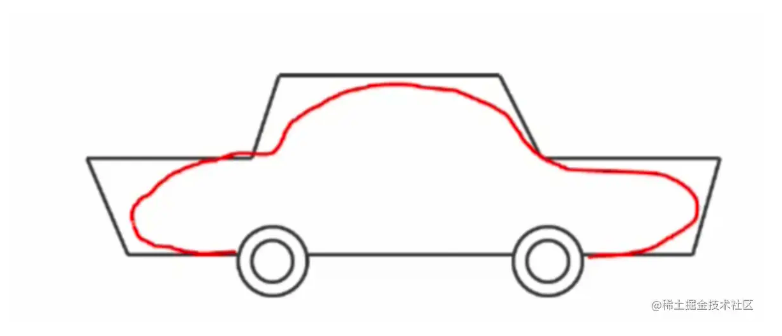
图1

这个方式是不是有点熟悉，刚看到的时候，我就想到了计算圆的面积时，我们会使用多边形来逼近圆的曲线（如图2所示）；贝塞尔曲线刚好相反，它是使用曲线来逼近多边形，刚好反着来了😂。

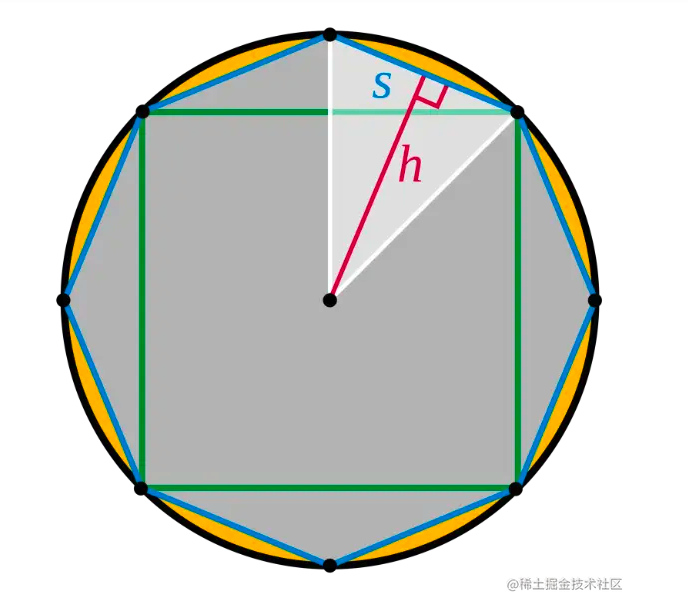
图2

构造贝塞尔曲线

思路虽然简单，但是如何把这个曲线画出来，或者说如何用一个函数来表示这条曲线就很困难了。不过这个不需要我们关心，有大佬已经解决了。我们直接来看看贝塞尔曲线的定义式，如下图3：

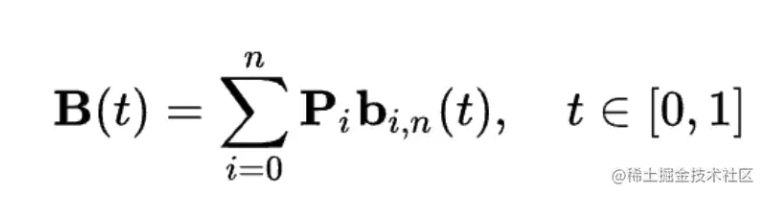
图3

先别急着划走，这个公式不用记，因为它太复杂而且计算量大，因此在工程开发中我们不会用它。一般在工程中，我们使用德卡斯特里奥算法（de Casteljau) 来构造贝塞尔曲线。听起来更复杂了，别急让我们举个🌰。下面以2次贝塞尔曲线为例。

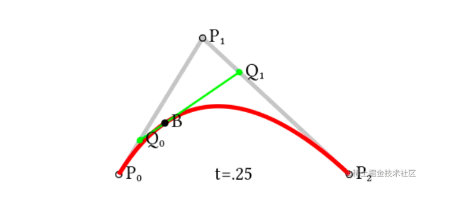
图4

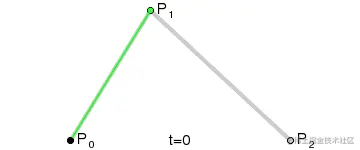
图5

看图4，德卡斯特里奥算法（de Casteljau) 的意义就是满足P0Q0P0P1=P1Q1P1P2=Q0BQ0Q1=t  \frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{Q_0B}{Q_0Q_1} = t P0P1P0Q0=P1P2P1Q1=Q0Q1Q0B=t 的情况下，随着 t 从 0 到 1 逐渐变大，B点经过的点组成的曲线就是我们需要的贝塞尔曲线了。图5是我们常见的动图，之前看的时候一直很懵逼，现在了解了贝塞尔曲线是如何画出来的，是不是清楚多了。

更高阶的贝塞尔曲线绘制方式和上面的一样，只是多了几条边，绘制的动图如下：

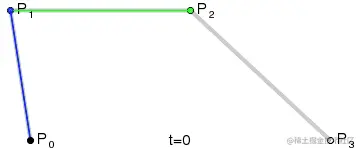
3次贝塞尔曲线

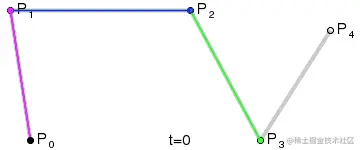
4次贝塞尔曲线

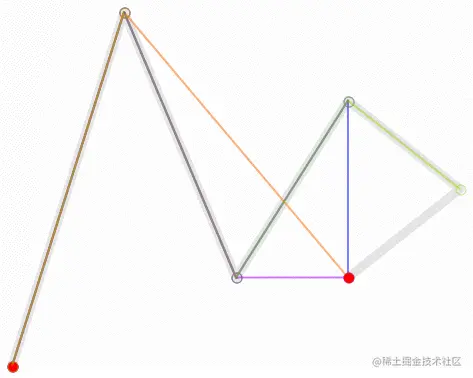
5次贝塞尔曲线

贝塞尔曲线的函数表示

看到这里，我们已经对贝塞尔曲线有了一个大概的了解。但是还是一个关键的问题，我们怎么画出贝塞尔曲线呢？或者说有什么函数可以让我们画出这个曲线吗？这个其实更简单，我们高中就学过了。还是以二次贝塞尔曲线为例，它的参数方程如下，其中 P0、P1、P2代表控制点。

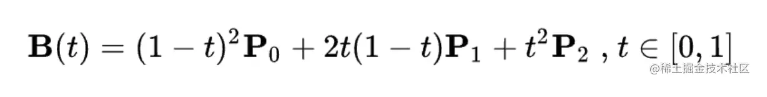
我们假设三个控制点的坐标是 P0 (-1, 0)、 P1 (0, 1) 、P2 (1, 0)，把值带入上面的参数方程，就可以得到如下结果：

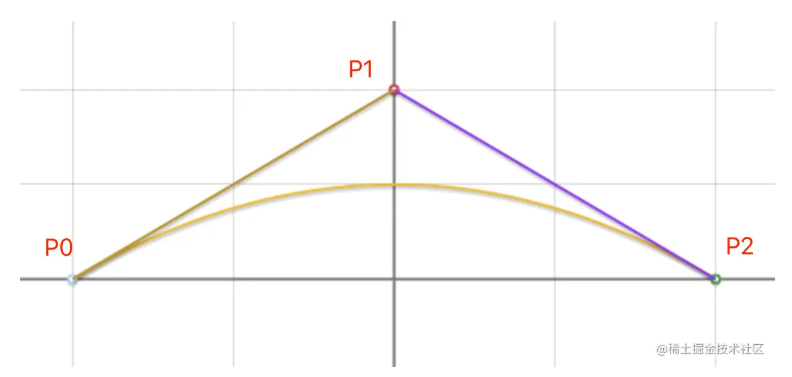
最后化解可得到我们熟悉的 y = f(x) 函数：y=−12x2+12：y = -\frac{1}{2}x^2 + \frac{1}{2} ：y=−21x2+21 效果图如下图。可以看出二次贝塞尔曲线实际上就是我们高中学的抛物线。唯一不同的是，我们高中求的抛物线，会经过 P0、P1、P2三个点，而贝塞尔曲线只会经过 P0、P1两个端点。

类似的：

一次贝塞尔曲线就是一次函数：y=a0x+a1：y = a_0x + a_1：y=a0x+a1 ；

三次贝塞尔曲线就是三次函数：y=a0x3+a1x2+a2x+a3y = a_0x^3 + a_1x^2 + a_2x + a_3y=a0x3+a1x2+a2x+a3

四次贝塞尔曲线就是四次函数：y=a0x4+a1x3+a2x2+a3x+a4y = a_0x^4 + a_1x^3 + a_2x^2 + a_3x + a_4y=a0x4+a1x3+a2x2+a3x+a4

n次贝塞尔曲线就是n次函数：y=a0xn+a1xn−1+...+an y = a_0x^n + a_1x^{n-1} + ... + a_{n}y=a0xn+a1xn−1+...+an

总结

贝塞尔曲线实际上并不复杂，我们可以简单的把n次贝塞尔曲线看成对应的n次函数的曲线。因为贝塞尔曲线的这个特点，也造成了贝塞尔曲线的最大缺陷————不能局部修改，即改变其中一个参数时会改变整条曲线。后面为了解决贝塞尔曲线的这个问题，提出了B样条曲线，下篇文章我们就介绍B样条曲线。

最后这篇文章为了方便读者的理解，省略了很多贝塞尔曲线特性的介绍，如果对贝塞尔曲线感兴趣，可以在B站上看看它的完整课程。